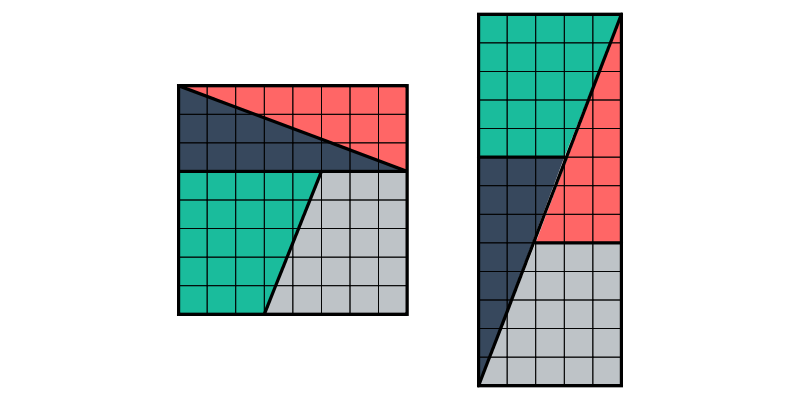
A favorite puzzle/paradox of Lewis Carroll based on Fibonacci numbers. The two figures are “obviously” composed of the same pieces, yet they have different areas!
> import Diagrams.Backend.SVG.CmdLine> {-# LANGUAGE NoMonomorphismRestriction #-}
> import Diagrams.Prelude hiding (tri)
> import Data.Colour.SRGB (sRGB24read)The standard infinite list of Fibonacci numbers.
> fibs :: [Int]
> fibs = 0 : 1 : zipWith (+) fibs (tail fibs)Create a grid by gluing together a bunch of squares.
> grid :: Int -> Int -> Diagram B
> grid x y = frame <> lattice
> where s = unitSquare # lw thin
> frame = rect (fromIntegral x) (fromIntegral y)
> # lw thick
> lattice = centerXY . vcat . map hcat . replicate y . replicate x $ sThe trapezoid and triangle shapes, with sides lengths based on two Fibonacci numbers.
> trap, tri :: Double -> Double -> Diagram B
> trap s1 s2 = lw none . strokeLoop . closeLine
> . fromOffsets . map r2 $ [(0,-s2), (s2,0), (0,s1)]
> tri s1 s2 = lw none . strokeLoop . closeLine
> . fromOffsets . map r2 $ [(s1,0), (0,s1+s2)]Draw the paradox diagram based on the nth Fibonacci number.
> paradox :: Int -> Bool -> Diagram B
> paradox n drawDiags = (sq # rotateBy (1/4)
> ||| strutX (s2 / 2)
> ||| rect # rotateBy (1/4)) # centerXY
> where f1 = fibs !! n
> f2 = fibs !! (n+1)
> s1 = fromIntegral f1
> s2 = fromIntegral f2
>
> trap1 = trap s1 s2 # fc (sRGB24read "#BEC3C7")
> trap2 = trap s1 s2 # fc (sRGB24read "#1ABC9C")
> # rotateBy (1/2)
>
> tri1 = tri s1 s2 # fc (sRGB24read "#FF6666")
> tri2 = tri s1 s2 # fc (sRGB24read "#37485D")The four shapes assembled into a square.
> sq = (if drawDiags then sqDiags else mempty)
> <> grid (f1+f2) (f1+f2)
> <> sqShapes
> sqDiags = (fromVertices [p2 (0,s2), p2 (s2,s1)] <>
> fromVertices [p2 (s2,0), p2 (s2,s1+s2)] <>
> fromVertices [p2 (s2,0), p2 (s1+s2,s1+s2)])
> # strokeP
> # lw thick
> # centerXY
>
> sqShapes = (traps # centerY ||| tris # centerY)
> # centerXY
> traps = trap2 # alignL
> # translateY (s1 - s2)
> <> trap1
> tris = tri1 # alignBL
> <> tri2 # rotateBy (1/2)
> # alignBLThe four shapes assembled into a rectangle.
> rect = (if drawDiags then rDiags else mempty)
> <> grid (2*f2 + f1) f2
> <> rShapes
>
> rShapes = (bot # alignTL <> top # alignTL) # centerXY
> bot = trap1 # alignB ||| rotateBy (-1/4) tri1 # alignB
> top = rotateBy (1/4) tri2 # alignT ||| trap2 # alignT
>
> rDiags = (fromVertices [p2 (0,s2), p2 (2*s2+s1, 0)] <>
> fromVertices [p2 (s2,0), p2 (s2,s1)] <>
> fromVertices [p2 (s1+s2,s2-s1), p2 (s1+s2,s2)]
> )
> # strokeP
> # lw thick
> # lineCap LineCapRound
> # centerXYDraw the order-4 diagram with thick lines in the middle. Passing the argument False causes the thick lines to be omitted, revealing the skinny gap in the rectangular assembly. Lower-order diagrams make the gap more obvious; higher-order diagrams make it increasingly less obvious (but make the grid smaller).
> example = paradox 4 True # frame 0.5> main = mainWith (example :: Diagram B)